Introducing Derivatives

The day that you first introduce derivatives is the most exciting day of Calculus!! (Well, at least WE feel this way as teachers!)  Here's how to spread that joy to your students.  Maybe they will discover why you love teaching this stuff so much!

To start out, take a day or two to just focus on the main idea.  You do not have to jump right into chain rule right away.  Give your class plenty of time to soak up the concepts.  Focus on "the slope of a tangent line" and "change of rate" vocabulary and main ideas.

Let your Students be Surfers for the day.

Dress up! (a fun surfer hairdo and a bandana will do!  Maybe throw some flowered shorts on over your pants.)

Decorate your classroom.  Spend two minutes finding a beach-themed or crashing waves screensaver to project onto the wall or whiteboard as they walk in.  Spend another two or three minutes drawing a huge surfboard on the whiteboard, or better yet, bring a real one to use for the lesson if you have access.

---

Get the class excited.  They are at the age where teachers do not bother to do this for them much anymore.  It will not take you much effort to make this really memorable for them, so go big!!

When you are ready to jump into the lesson, start with a large graph.  A quadratic function works well.  Draw or find a graph of a parabola that opens downward, since that is the easiest to compare to a wave.  Demonstrate how the surfboard can travel along the curve.  Explain that its slope at any point is the derivative of the function at that point. 

Resource #1: "Function Surfer" Applet for Derivatives

Project this "Function Surfer" applet on the board or let students explore in pairs if you have the technology for everyone.  This applet is great for them to play with while they explore the surfing analogy.

Resource #2: Printable Surfer Dude 

Here is a little surfer man I put together for students to use.  Ideally, you want to print this on a transparency so that he can "ride" along the graphs on worksheets and students can still see the curve.  If you cannot do that, just print on regular paper and have students cut along the straight line at the bottom of the surfboard.  Click on the image to download the PDF.  Four surfer dudes print per page.

These guys are great to use along with Resource #5 below as the "straightedge" needed in the inquiry activity.

Resource #3: Derivative Infographic

This Derivative Infographic is available in my store and displays the main ideas for understanding derivatives. 

For one dollar, you can print it forever for all of your students every year until the end of time.  Click the image to check it out.  It prints two-per-page with an option of color or black and white. 

It is great to hand out as a bookmark and can be laminated or three-hole punched for binders.

---

Connect With Physics

If all your students happen to be taking Physics, try collaborating with the Physics teacher to make the connections.  If not, just incorporate it in your own classroom.  I think the best way for students to really understand the relationship between each derivative and the rate of change is to work with position, velocity, and acceleration.

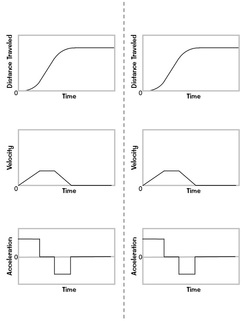
Show a position graph and explain what it represents.  Write "position" on the board.  Ask students to come up with a word for how quickly position changes.  Write "velocity/speed" below the word "position."  If they need help, act it out.  Walk slowly, then fast across the room.  Then ask "Ok, is there a word for how fast the velocity changes?  Have them think about slowing down and speeding up when driving.  Write "acceleration" below "velocity" on the board.  Display or hand out graphs for position, velocity, and acceleration.  You can even talk about "jerk" as an opportunity to go one more level to incorporate a third derivative.

The key here is getting students talking out loud or writing in complete sentences.  Try to get a real discussion going.  Encourage students to clearly verbalize the relationships.  Have them look at the position graph and talk about it.  You need them to speak out loud and hear classmates say plenty of statements like:

- "The car must be going faster here because the position is changing more quickly than it was." 

- "When the velocity starts increasing more quickly, this means that the acceleration is increasing."

- "The car is driving at a steady rate (constant velocity) when the position graph is linear.  The slope is constant, so the position is changing at a constant rate."

- "The car is stopped when the slope is zero.  The position is constant."

Have students take time to really look in-depth at each graph and point to the different intervals and explain out loud.  Make connections by labeling the position graph f(x), the velocity graph f'(x), and the acceleration graph f''(x).  Start using the words "first derivative" and "second derivative" to introduce the new vocabulary.

Resource #4: Position, Velocity, and Acceleration Graphs

This PDF has graphs for distance, velocity, and acceleration for your students to analyze.  Print one strip for each of them (two will print per page).  Once they have looked and talked through the graphs, they can run their surfer dude along the curves to investigate the slopes. 

When they are ready, you can try giving them the second page of the PDF, which has a distance graph to start with, but blank velocity and acceleration graphs.  Challenge your students to complete the graphs.

Click the image to download.

Resource #5: Inquiry Activity: Graphing the Derivative of a Function

This three-page worksheet guides students to graph the derivative of a function.  The activity is set up as a guided inquiry.  Students do not need to know how to differentiate.  This is a great introduction to the graphs of derivative functions.

When your students do the graphing in a hands-on way and make discoveries about the relationships, they will understand and remember the concepts.

In this activity, students answer critical thinking questions in complete sentences and make discoveries about the degree of f(x), f'(x), and f''(x).  They use a straightedge and find slopes of tangents along the curve to graph the derivative function.  The PDF for the "Graphing the Derivative of a Function" inquiry activity is available in my store.  Click the images to check it out.

I hope your students love the derivative lessons! Enjoy!!

To Read NExt: