This is best BEFORE teaching how to find asymptotes and graph rational functions.
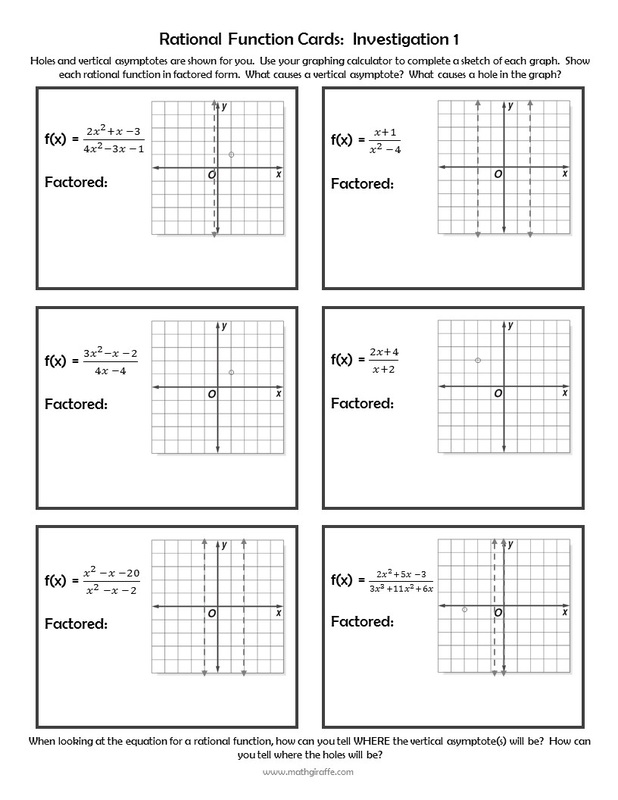
Start with just a 5 minute introduction to what an asymptote means and what it looks like. Then, the kids jump into Investigation 1.
The kids analyze the factored forms of the functions and figure out what is causing the vertical asymptotes and holes.
Then, the second investigation follows with horizontal and slant asymptotes.
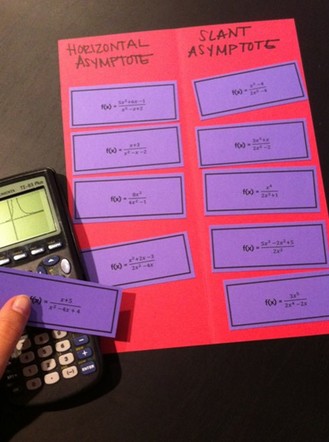
For this one, I made a little reference "cheat sheet" for the students. If they do not recognize what is happening on the calculator screen, they can take a peek at these samples.
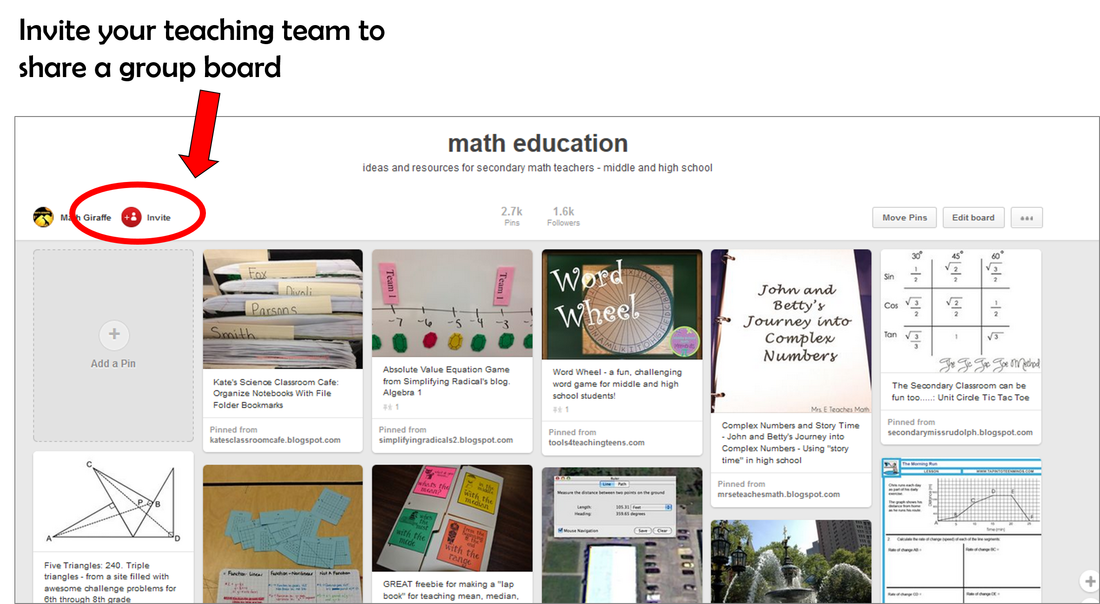
For both parts of this activity, it works best if you have the students cut the cards apart. This way, they can separate and differentiate them. Then, they can look at each "collection" and start to hunt for the patterns and characteristics of each feature.
I like to have the kids work in pairs.
Click here to download all the files for the "What Makes an Asymptote" Investigation lesson.
Looking for more great high school math resources? Enter your email to get some sent straight to your inbox!
You may also like...
1 Comment
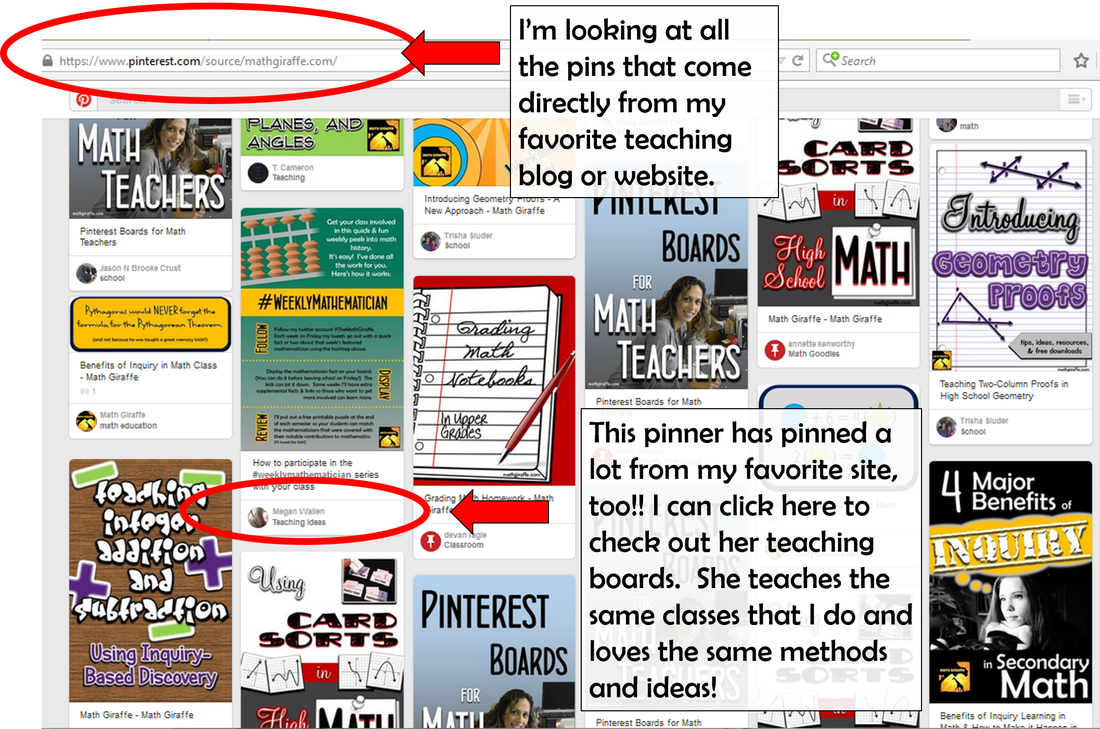
Finding It
Tricks for finding those PERFECT ideas that will fit YOUR particular classroom and content needs
Saving It
How to make sure you don't lose that idea that you loved, and how to remember the inspiration it gave you
Taking Advantage
Tips for really utilizing all of the features and extras that are built-in on Pinterest
You may also like...
Secondary Smorgasbord Linky
8/12/2015 5 Comments 4 Major Benefits of Inquiry Lessons & How to Use Them to Help Your Math Students Thrive
1. Inquiry enhances independent problem solving skills.
Inquiry-based learning teaches students how to find patterns, figure out properties, and discover new rules of mathematics. They slowly learn how their brain actually progresses through the idea to get them from "lost" to "ohhhhh, I see what the pattern is." After this becomes second nature, they will be more ready to attack future unknown situations.
The critical thinking skills that are required to ask questions that will lead to discovery are learned and acquired. They develop through practice, just like any other skill. Students must practice the inquiry process, just like we as teachers must practice sitting back and letting them struggle. It's not easy, but begins to feel more natural over time. As students get more and more accustomed to the inquiry structure that you use, they will slowly strengthen their own skills and gain independence in problem solving. Here's an Algebra example: I always teach exponent rules with guided inquiry. We work through the patterns and write out all the variables and cancel or expand until students develop product rule, power rule, and quotient rule for themselves. Then, when we get to the negative exponents later in the unit, their skills with this process have grown to the point that they know how to come up with their own concrete examples. They know how to look for patterns. I have them develop their own sets of rules for negative exponents.
Work towards the skills that will lead your students to persistence in problem solving.
2. Discovery leads to deeper understanding of a specific concept.
After discovering a mathematical property on their own, students will truly understand the concept behind the rule. Instead of following a set procedure, they will understand WHY a rule works and HOW it was developed.
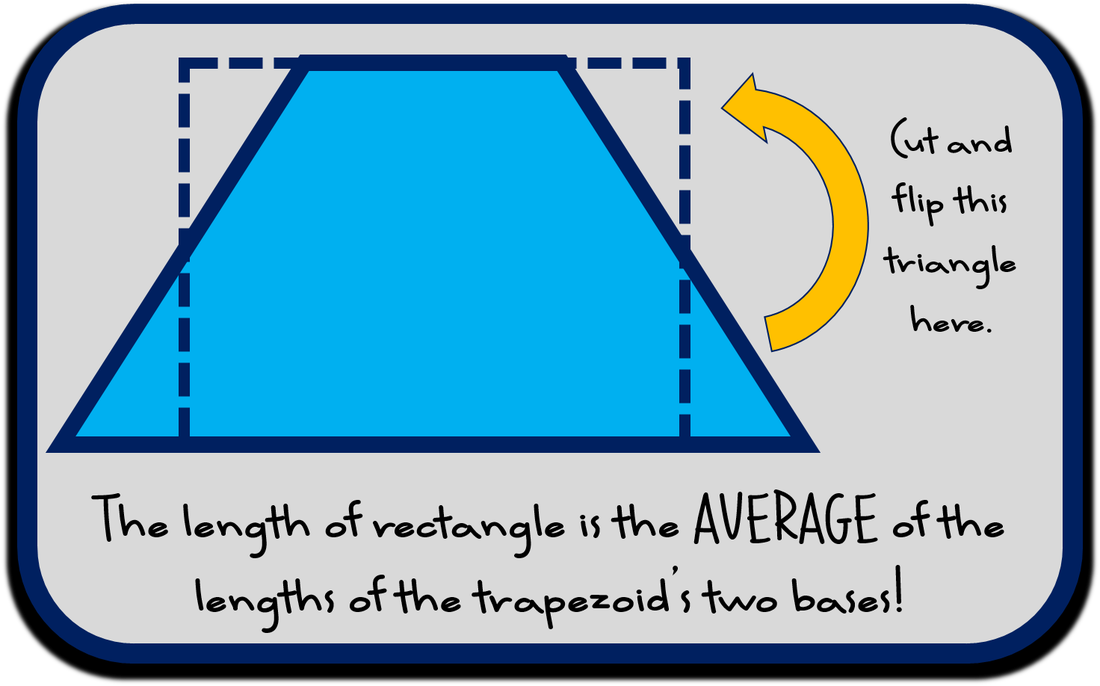
Let your students build a concept, not just follow a given process. It's very rare that I give a formula as a part of notes. I like to have students find a formula for themselves. One example is for surface area of a cylinder. I have a dissection lesson for classes to "dissect" a cylinder "specimen." They have to discover for themselves that the length of the rectangle is equal to the circumference of the circle, and then go from there. Most middle school students across the world REALLY struggle with truly understanding this formula. They have a hard time visualizing the base and why circumference plays a part in this formula. However, after this hands-on lesson, the students really "get it" and never forget how the rectangular face wraps around. You can read more about this lesson in my Cylinder Dissection blog post. I do a similar structure for discovering circle theorems in High School Geometry. Students draw their own chords and have to tell ME how arcs, tangents, central angles, and inscribed angles are related, instead of me telling THEM these theorems. 3. Students discover a new level of math confidence & self-motivation.
When students feel the pride that comes from discovering a theorem, property, or formula for themselves (just like a mathematician does!), they suddenly gain a new level of confidence in their own math abilities.
I have noticed students have a sudden willingness to try a new challenge or approach a different type of problem instead of giving up. Kids believe in their ability to apply knowledge from one situation to another. I feel like this has given my students huge advantages on standardized tests. After I started incorporating more and more inquiry learning, the kids got more and more comfortable with being exposed to an unfamiliar problem type. 4. Retention increases HUGELY when concept mastery replaces memorization.
This is so important to note, and one of the benefits that I rarely see advertised by supporters of inquiry learning. Here's the thing:
If a student develops a formula, rule, or property for himself, then he understands on a deeper level where it came from. He won't have to memorize it at all.
The student can reproduce the formula at any time because he "discovered" it. This is especially true if it was done in a hands-on way. During a test, or later in life, the development of the idea is what will help a student recall how a property works or how to re-create the formula. So, here's how to make it happen in your classroom:
Some tips as you start to incorporate more inquiry learning, and give your students these benefits -
Like it & want more? Subscribe to my email list:
or check out these other posts:
|
Archives
December 2023
Click to set custom HTML
|



























 RSS Feed
RSS Feed