Why Bother Taking the Time to Go Hands-On?
Dr. Ben Mardell, Phd with the Project Zero at Harvard University has said, "kids learn through all their senses and they like to touch and manipulate things." Basically, hands-on activities activate more regions of students' brains.
It’s actually pretty simple. As Judy Dodge author of 25 Quick Formative Assessments for a Differentiated Classroom states "The more parts of your brain you use, the more likely you are to retain information, if you're only listening, you're only activating one part of the brain," she says, "but if you're drawing and explaining to a peer, then you're making connections in the brain." That’s why things like doodle notes and hands on activities are so important. Activities like these are easy to implement and immensely beneficial to the students. 1. Cut & Paste
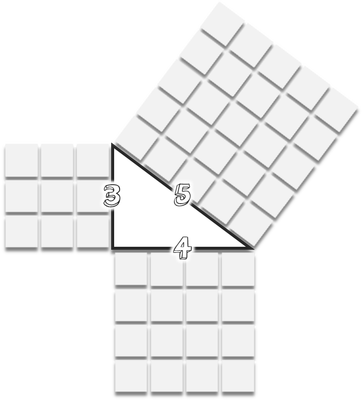
It can sometimes sound rudimentary, but a simple cut and paste activity is a tried and true method of learning. Kinesthetic learning is a great way to engage your students. Have your students cut up diagrams or models from worksheets or even a photocopy of textbook samples.
Then have your students arrange them on paper and scotch tape them down to create the original, then re-number and write/tweak the actual question (save time drawing the diagram or model yourself). Here is a great example of a hands-on pythagorean classroom activity from Kyle Krafka. 2. Folding
Another great illustration of the Pythagorean theorem is through paper folding. By folding a plain sheet of paper your students get a first hand look on exactly how this theorem is applied. This one moves fast, but is really spiffy!
This origami-style activity will help your students see and remember how the theorem actually applies. The great part is that it is a general proof that works for different right triangles, and you can actually fold further to get different versions. 3. Project: Create a 3-d Model
Have your students team up in pairs and create and actual 3D model of the theorem. They can use small balls, blocks, jelly beans, water, or even wadded up balls of paper to show how the side lengths work out. Here is an example that a few students came up with in their own math project.
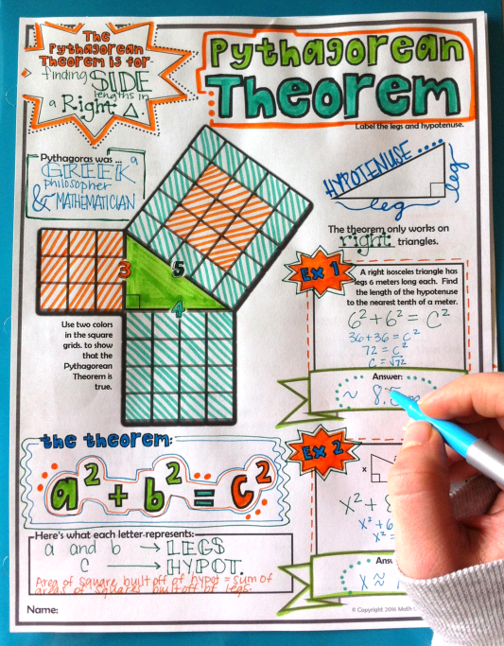
4. Concept-Based Doodle Notes
This set of doodle notes is a great way for students to record and reference the basics of the Pythagorean Theorem. Visual note-taking is a strategy that is as hands-on as notes can get, and has been proven to boost focus, learning, and long-term retention.
Teaching fundamentals is extremely important. However, what you really your students to retain is the real meaning of it all.
Taking concepts such as the Pythagorean Theorem out of the text (beyond just memorizing a formula) and into our hands is a wonderful way learn. Do you have any tips or tricks you use in your classroom? Let us know what you do in the comments below! Enter your email address to get future articles, free lessons, updates, and more math education ideas: To Read Next:
13 Comments
2/23/2017 0 Comments Integrating Learning Across Subject Areas: WHY & HOW to Make Cross-Curricular Teaching Happen
One of the early records of this idea can be found in 1899 in John Dewey’s The School and Society, where he said, “Relate the school to life, and all studies are of necessity are correlated.” And what isn’t a surprise is that it’s incredibly beneficial for our students too.
It’s no secret to teachers that students have different learning preferences and interests. They may zone in and out of a subject that they aren’t crazy about, but focus attentively in another. When certain concepts are taught in more than one classroom, students will grab onto that information at some point. If they missed it in morning reading, they may get it in afternoon math. Middle school students are just really starting to dive into learning and how it connects to the world around them. And the world around them also consumes most of their attention. A lot of times they aren’t super focused on school. That’s why an integrated curriculum works so well with middle school students. How Our Middle School Students Benefit from Integrated Curriculum
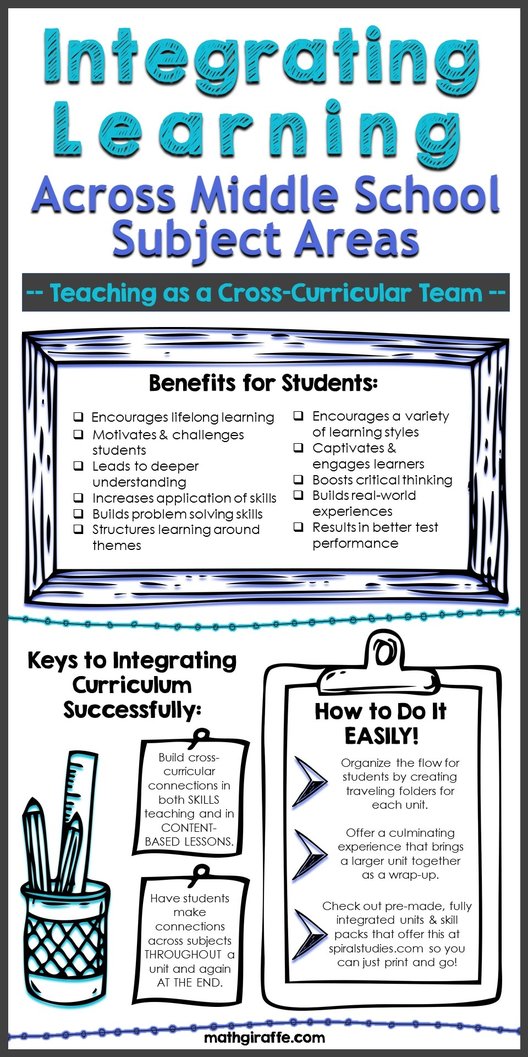
When you teach a themed-based unit students can learn math, science, social studies, and reading all at one time. And it’s not overwhelming for them either, it’s actually the opposite. Students not only connect and create real world connections, they are also more engaged in the classroom. Here are just a handful of the benefits:
● Encourages lifelong learning ● Motivates and challenges students ● Deeper understanding of concepts ● Application of skills that are learned ● Builds problem-solving skills ● Structures learning around themes ● Hosts a variety of learning styles and theories ● Captivates learners ● Better test performance
When students know that the things they are learning actually applies to more than just one lesson in a classroom, they end up being more motivated to learn it. It strengthens their willingness to learn it as well as their ability to retain the information. By making connection through real life or across different subjects, learning is fused together to make a more fulfilling and tangible learning experience for our students.
ADDED BONUS: Integrated curriculum offers repetition of information, but with variety! John Medina, a renowned molecular biologist stated in his book, Brain Rules, that “the capacity of memory is initially less than 30 seconds. If we don’t repeat the information, it disappears.” So basically, a lot of what we are teaching them is just going in one ear and out the other. Medina continues and states, “the way to make long-term memory more reliable is to incorporate new information gradually and repeat it in timed intervals.”
By teaming up with other teachers and incorporating various subjects throughout the day, students will encounter some of the same information. It will reiterate important content that students may have missed or forgotten from previous lessons. Students can hear the information in the morning in one subject, then that knowledge is refreshed later in the day during a different class, making them far more likely to remember what is being taught.
However, part of the problem with integrated curriculums is that it can be hard to create an effective way to present it to our students. And that’s where Spiral Studies come in. We’ve combined our expertise to make absolutely turn-key integrated units for you and your team. We make it easy for teachers to connect the subject areas by planning and developing cross-curricular units, lessons, and skill packs for grades 6-8. All you have to do is print and integrate! Check out all of the details and get the material here!!! This team and our materials make integrating a breeze. You'll be stunned how well-coordinated these are.
Looking for more ideas, teaching strategies, articles, and resources? Enter your email address here to get updates & printables right in your inbox:
To Read Next:2/23/2017 3 Comments KEY SKILL: Teaching Students to Test Cases And Use Examples & Counterexamples in Math Class
The easiest and most concrete way I've found to do this is through "always, sometimes, never" questioning.
Kids cannot think through these types of questions without mentally testing cases. And if you go a step beyond to have them support their answers, they will be forced to justify by using both examples and counterexamples. BONUS: This type of question almost ALWAYS inspires some solid "math talk," so make sure to let your classes work in pairs or showcase their reasoning at the board to get that conversation going. Here are some examples to try to incorporate: Testing Cases in Algebra:
Often, students may think they know the answer and then in testing, they'll come across a different situation that violates the "rules" they were imagining originally.
Make sure to have them try every case they can think of that fits the "premise" criteria and then see if they can reach a conclusion about whether each statement is always true, sometimes true, or never true.
Samples with Quadratics: Always true, sometimes true, or never true??
Pre-Algebra Examples:
Have kids try these samples, and be sure that they support their claims by providing both examples and counterexamples.
See if they can develop some systems to organize their work and be sure that they have tested every possible case.
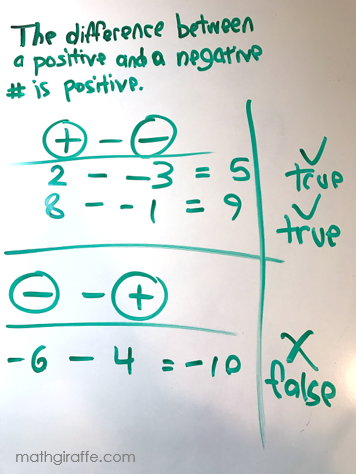
Samples with Integers: Always, sometimes, or never true??
Students will need to test in different orders and justify their answers by showing each case and whether it turned out to be a true or false statement.
Geometry Challenges:
These ones work well at the board, because students can watch one another draw the figures and see which cases work out.
If you have access to geometry software like GeoGebra, you can use that as well. Have students draw each triangle and see if they can drag a vertex to meet the criteria.
Samples with Triangles: Always, sometimes, or never true??
Best Ways to Try It:
All the sets I develop with this type of questioning include 36 statements to classify.
My favorite 2 ways for students to work through these types of questions are in partners in a worksheet, or as teams with a sorting activity with a notebook on the side. PARTNER WORKSHEET: I lay the statements out in a grid so that when they color each statement that is NEVER true RED, each statement that is ALWAYS true BLUE, and each statement that is SOMETIMES true PURPLE, it creates a pattern that I can check really easily in just 2 seconds. This makes it really easy to check it over as I walk around and just point to ones that I can see are incorrect. They go back to the drawing board on those statements and continue their (sometimes heated) discussions!
SORTING ACTIVITY:
I cut the statements (larger print version) into cards and have small teams or pairs of students sort them into categories based on whether they are always, sometimes, or never true. Be sure that they have notebooks available, because at any moment they may be required to provide examples to support their answers. You can also hand out the cards and have students come up to the front in a whole-class setting to tackle challenging ones. These are pretty versatile. It's nice to hear a student model an explanation and show the class how they tested different cases to reach a conclusion. Get Pre-Made Sets
Each time I develop a set, I pull together my worksheet version and my sorting version so both are included.
Browse the sets that will work well for your classroom and get your kids thinking critically! Pre-Algebra: Algebra: Geometry: Get Inspired:To Read Next: |
Archives
December 2023
Click to set custom HTML
|























 RSS Feed
RSS Feed