|
11/24/2014 7 Comments Infographics for Education
In this fast-paced world of instant access to information, infographics have become popular for displaying statistics and facts.
Take advantage of this trend to give your students a great visual tool! After seeing this format of informational displays all over pinterest, I noticed that most of the available infographics were used persuasively. I saw plenty of environmental and political data as well as great stats for a wide variety of topics. I decided to start putting together some educational infographics that could be used in the classroom to display content. Math students LOVE having these as a reference. They are so helpful for my visual learners.
I have also collected some sites and tools that will help you and your students to develop some great infographics and start taking advantage of this idea right away!
Student-Created Infographics
One way to incorporate infographics into your classroom is to assign your students a short project in which they develop their own infographic. This works great in any subject area and is a great way to integrate technology education into your curriculum. You can offer this as one option when you differentiate using a choice board or you can require all students to make an infographic.
You can give a very specific list of what must be included within the topic or allow students a little more freedom. Here are a few samples:
Here are some sites and tools that your students can use: * Piktochart (a free tool for designing infographics) * Easel.ly (a free tool for original content) * Classroom Clipart (free images for students to use) Note: These are NOT for commercial use. Please make sure each is appropriate for your students and grade level before using. Teacher-Created Infographics
Another option is to create an infographic yourself and print it for students.
You can place any information that you feel is most important for them to remember about each topic. Students really love having these as study guides. They can remember the concepts because they can visualize the way that the infographic presented the information.
Click here to visit my "Infographics" category within my store. They are available for just a dollar, which entitles you to unlimited printing for all of your students FOREVER! Check them out or have fun creating your own!
I leave a space on the left of each tall half-page, so we can easily 3 hole punch them for binders.
For more ideas, updates, and free resources, subscribe by entering your email in the sidebar.
To Read Next:
7 Comments
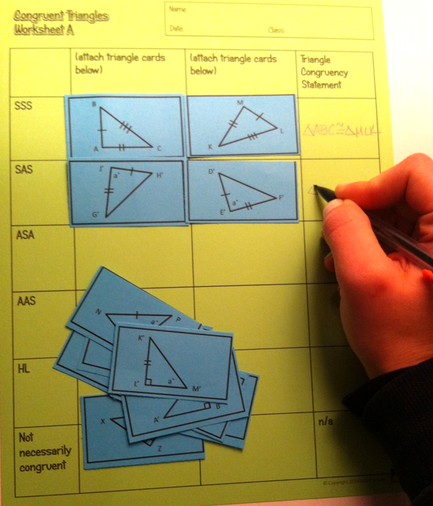
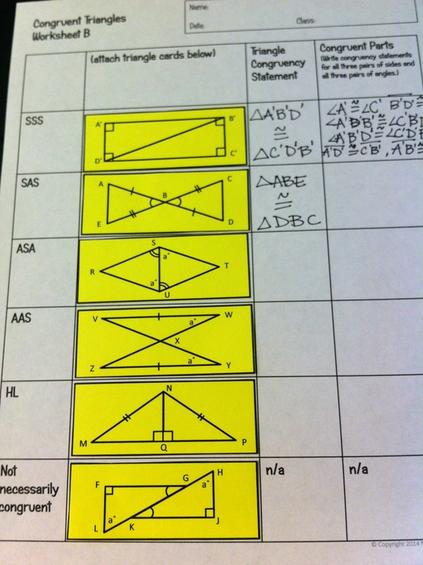
11/22/2014 26 Comments Discovery: Congruent Triangles
They can thread one of each length onto a piece of yarn and tie it off to create a triangle. Challenge them to create a second triangle with the other three pieces that is NOT congruent to the first. (They discover SSS for themselves)
Next, use a paper clip to fix an angle between two straw lengths, and challenge them to again create another triangle. Continue the process, going on to ASA and SAS.
I like to have students record their observations by writing a conditional statement of their own explaining their discoveries for each pair of triangles. Give them only this structure as guidance: If ____________, then _______________. After the hands-on investigation, have students share the rules that they wrote for congruent triangles. Clear up any misconceptions and give notes on notation, order of vertices, etc. I talk about why AAA and SSA are not sufficient to prove triangles congruent. We also discuss HL and AAS. On a block schedule, this all can fit into one class period, but on a traditional schedule, it makes sense to break congruent triangles into a couple of days. I like to set up practice afterward in a way that leads smoothly into proof writing. I require them to write congruency statements, identify all the corresponding parts, and work with complex diagrams with two triangles, like they will see later on. This helps lead them into the next steps more easily. Here's my practice pack. To Read Next:
11/22/2014 4 Comments An Algebra Version of Infant Dot Cards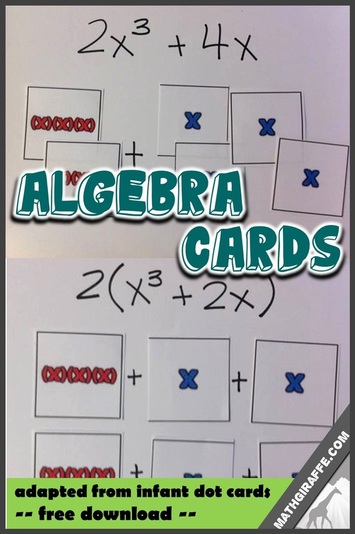
I have a beautiful baby girl, and when she was only about a month old, I came across another mom's blog that caught my attention. This mom was interested in the "Doman" philosophy for parenting and education, based on Glenn Doman.
I looked into Glenn Doman's books a little further and discovered a book about teaching math to very young babies. As a math dork, I had to check it out. The book recommends using "dot cards" for teaching numbers to babies. It turns out that infants can look at the dots and recognize the quantity. They can identify very large numbers without knowing how to count and without knowing any numerals. 
The book suggested creating or printing the dot cards (PDF available here) and showing them to the infant while saying the number. After slowly adding cards in each session, the infant has a concept of which set of dots represents each number.
Eventually, it has been proven that the infant can understand simple equations that are set up using the dot cards, such as the one in this image.
All of this is done before introducing the child to the numerals that we use to represent numbers. I really enjoyed the book and found quite a few fascinating facts and ideas in it. However, it got me thinking about using this type of visual representation for older children.
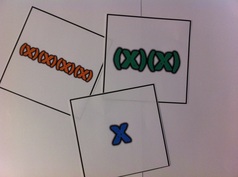
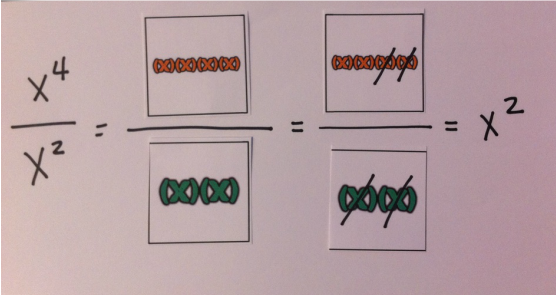
It made a lot of sense to me that these cards are a better way to introduce an equation than writing 4 + 5 = 9. The symbols that we use to represent mathematics can be abstract. We have assigned numerals to the quantities, but they are not necessarily intuitive to children. A child or baby can understand addition better visually (by seeing the dots). I realized that we already know that this is true for many older students as well. In Algebra, we also assign symbols to quantities. I decided to try to adapt the dot cards to a similar style of visual learning cards that could be used for representing algebraic expressions. Laws of Exponents
I realized that the Doman method was similar to the way I already like to teach the laws of exponents by rewriting each expression as a product of its factors, but instead of writing out each expression, I could use my cards. They can be put up on the whiteboard while I have students expand the expressions. The cards are a great visual representation to help show why the exponent rules work.
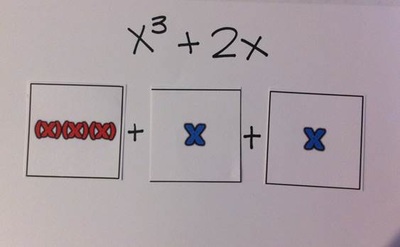
I started thinking of other ways to use these cards to represent different concepts. I put together a large set to stick up on the board and a small set to use as student manipulatives. I used different colors to help students remember to differentiate like terms. These will be great for teaching the distributive property and polynomial addition, because students can represent an expression, then pick up the pieces to move them and regroup them.
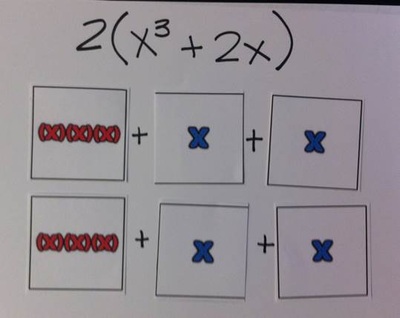
The Distributive Property
Here is a sample showing that "two of this quantity is really represented by two of each term."
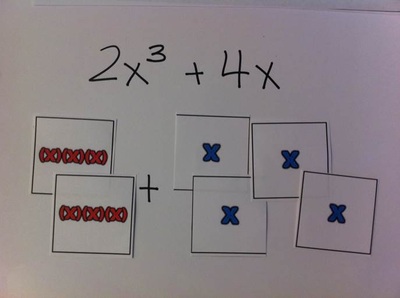
combining like terms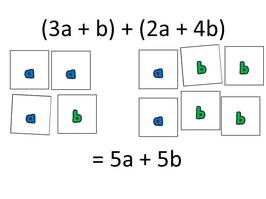
When I taught middle school, I liked to color code the like terms in expressions by drawing colored boxes around the terms. I think these cards would be even better for visualizing the redistribution of the terms. Students can move the pieces around and really see that the groupings of the individual variables are changing when they combine like terms.
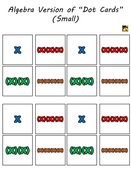 Download PDF Download PDF
I am sure that there are tons of other applications for these cards. Download the cards by clicking on the picture! I have included the large cards for the board and the small set to print for your students. Combine them with the Doman dot cards (can be used to represent constants). Leave a comment to let me know if you thought up some other ways to use these in your class.
Here's the affiliate link to the book I read. Check it out if you have little ones and a math mind! To Read Next:
|
Archives
December 2023
Click to set custom HTML
|


















 RSS Feed
RSS Feed