Great news!  The Pre-Algebra full course of doodle notes is now available in printed hard copy paperbacks!  Yep, I've gotten it officially published and you can now order copies to get shipped right to you.  Your school can order these for your classroom through Barnes & Noble here.  This is a great way to purchase a class set, and receive one book per student.

This option is also wonderful for homeschool, since you can pay per student rather than purchase the teacher license for the digital file.  Those digital licenses that have already been available on TpT are per teacher and entitle you to print for all your own students each year.  This is still an option, and is very cost effective for teachers with entire classes of students who are willing to print and copy pages themselves.  But this new paperback, on the other hand, must be purchased for each student.  Copying is prohibited.  It's a high quality book with sturdy paper all bound in one place for students to keep as a workbook of doodle notes for all 10 chapters of middle school Pre-Algebra content.  If you have any questions about the two options, just let me know. 

When students start out with any confusion at all with converting between congruence statements and equations, they struggle through each next step all the way through proofs.  Take time to tackle this key skill before moving on.

As a geometry teacher, this pet peeve that would pop up over and over again: I'd be grading and see students mixing up their usage of congruent and equal in lines of a proof.  Since I make kids write out separate lines for each step, including converting from a statement of congruence over to an equation with the measures, missing this was really messing up their scores, along with driving me crazy.  Every class, with no exception, would continually mix these up for weeks on end.
 
Eventually, I discovered that it was worth taking time to explicitly teach this skill.  We took a while to practice converting between the two types of statements.  I explained how when you describe figures you use the term congruent, and when you are describing numbers you use the term equal. 
 
We had to bother to take time showing how to switch back and forth between a statement like "length AB = length BC" while saying aloud "The DISTANCE between A and B is a NUMBER!" and a statement showing "SEGMENT AB being CONGRUENT to SEGMENT BC."  Talk these through out loud before assuming that students can see the distinction.  Practice converting back and forth before you allow them to actually use these statements in a Geometry proof. 

​Trust me, it is worth the time.
 
Otherwise, you’ll see hybrids such as <2 = <5 over and over again, which leads students to stumble between steps in their proofs.
 
It helps to display a Reminders poster, like the one below in the room. 

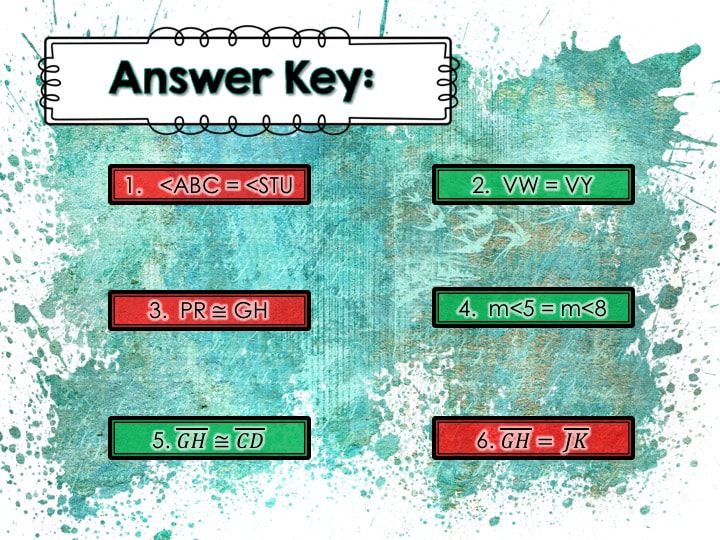
​Then, after practicing a few examples, we work on determining if a statement uses congruent or equal correctly with statements like the ones below.  
 
Lastly, I’d pull up the answer key, and we would discuss why each statement was either correct or incorrect.

Here is a PDF dowload version for you if you'd like to use them too.

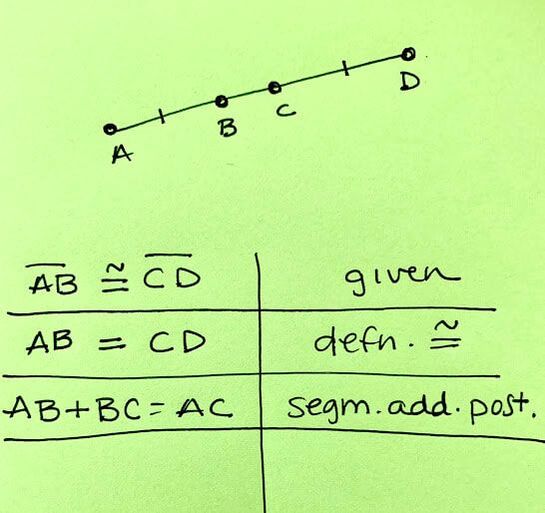
This really comes into play in examples like the following proof:

Students MUST convert from the congruent notation in the first line into an equation in order to use substitution later on in the proof.  Segment addition postulate does not blend with congruent statements.  It only works with statements of equality, since addition is required.  To work in an equation format, which is necessary in many proofs, students need to be able to smoothly switch from congruence statements into equations and vice versa.

Hopefully these short little downloads and this tip will help you prioritize this skill and take 15 minutes now to save yourself many future headaches and give your students a boost to help them through proofs.  What's your own pet peeve when grading proofs?