|
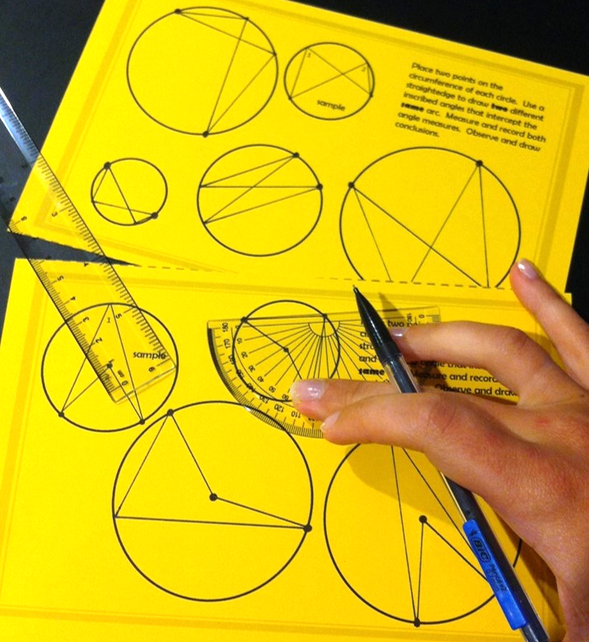
11/17/2022 13 Comments Teaching Circle TheoremsHow to Teach Properties of Circles for Deeper Understanding & Stronger Retention* (Note - Don't miss the free download at the end of this post.) In high school Geometry, we need students to not only be able to use theorems properly in proof writing and problem solving, we need them to also understand them on a deeper level and be able to reproduce them as needed. We also want them to be able to recall the theorems easily so they know which one they have to use. The way to do this is not just through lecture, then memorization! There are a lot of circle theorems, and to your students, it probably feels like they all just blur together unless you really strategize the way you teach them. To introduce new theorems in a way that students can integrate them into their conceptual understanding of how Geometry works, we can use a few strategies. To increase both deep understanding and retention (memory) of theorems, you'll need to: 1. Have students discover the theorems themselves. They'll need to investigate, explore, and actually see the theorem come to life through an inquiry process. Whenever you can use an investigation to allow students to discover properties themselves, understanding of the deeper concept behind a mathematical property is increased. This way, students are able to reproduce the rules, formulas, and procedures for themselves without memorizing because they understand where the rules came from. (A side bonus of using inquiry is that students get a boost in their problem-solving skills. They gain resilience to stick with a challenge and learn to think it through for themselves and develop stronger critical thinking abilities.) For more information on how and why we want to use a discovery lesson as an introduction, check out my inquiry learning page. 2. Engage both brain hemispheres and activate the benefits of dual coding theory. By blending graphic (visual) information with auditory information / words, you'll help students make neural connections that allow them to convert the lesson into long-term memory. You'll see how we do this below, but be sure that you check out my doodle notes hub if you are new to using creative visual note-taking methods in math class. 3. Use color-coding. Colors and color combinations can have an effect on attention and memory. Neuroscientists have found that color is one of the first things to register in our brains, and has a pretty strong impact on learning. Geometry is especially conducive to color coding. Get students in the habit of always having multiple colored pencils out on their desks, and have them always use different colors to mark up diagrams any chance they get! Step By Step Plans: How to Teach Circle Theorems*(First, a quick note: All the specific materials shown in the images are here, so you can get them all in one place and then grab the free download at the end of this post to use in your classroom.) Review definitions if needed before starting. If your students are not confident with naming the parts of a circle, you'll want to go over the vocabulary before throwing them into working with the theorems. It's difficult to understand new theorems if you don't have a good handle on the terms first. Build familiarity with a quick review of the parts of a circle. Doodle notes are a great way to do this in a way that will solidify the meanings of the vocabulary terms in long-term memory. For example, if you have students do their notes as shown below, they'll benefit from the hand-to-mind connection. They'll recall how they filled in the sector with the word "sector" in large letters, and how they wrote or doodled the words "arc" and "circumference" in a curved way and added doodles around the circle to extend it around the entire circumference. They'll remember using one color for all the straight line segments, hand lettering for areas within regions, and another color for the curves. The act of coloring, doodling, sketching, color-coding, or hand lettering their vocabulary terms helps them to convert the words to long-term memory. If your students already are strong in these definitions, you can skip this and move ahead to the investigation. Kick it all off with an investigation lesson Before you do any lecture or notes to introduce circle theorems, allow your class to explore them through a discovery lesson. By developing the rules for the properties themselves, they will actually see how and why the theorems work. They'll understand where these theorems came from when they discover them for themselves. This type of activity works great in pairs. Have students work with a partner to go through the investigation lesson. They'll discover 4 of the circle theorems themselves, using a protractor and straightedge. For example, have your students draw 4 or 5 circles of all different sizes using a compass. Then, direct them to place two points on each circle. Have them draw two different inscribed angles that intercept the same arc. They'll take time to do this for all their circles on their own in pairs, record the measures, and start to make their own observations. Think of it like a science lab. They will look for patterns and see if they can draw any conclusions. Of course, their results may not be perfect. One angle may be 57 degrees and one may be 58 because of variation in the perfection of their lines and their protractor skills and estimations. But by doing it enough times throughout the exploration, they'll start to see some similarities and begin to guess at the property at play. When you teach using inquiry, your most important job is actually to sit back and resist the urge to teach! This can be harder than it sounds. You may need to give supportive hints here and there, but only if a group is truly stuck. Otherwise, make them struggle. It's ok if it's difficult, and you can remind them of that. It's a productive struggle, and they will have stronger learning because of it if they push through. Sometimes they're so used to being spoon-fed the content, that they beg for help and insist it's too hard, but have not really made a real attempt to figure it out themselves. Find the sweet spot where you are being supportive, but without offering them any substantial help. They'll do ok once they see that you really are not going to step in and do it for them. Some students will take longer to get to the point that they realize they really are on their own, but once they see that they really do have to figure it out for themselves, they'll be able to. Just be encouraging. A guided inquiry like this one helps walk them through it so they don't feel quite so lost. Then, they'll write up sentences officially stating the theorems they discovered. My lessons have them do only 4 on their own through investigation. They write those into their booklet where they record the theorems, and then they eventually just will complete the rest of the theorems that are provided for them to eventually cover these 10 theorems:
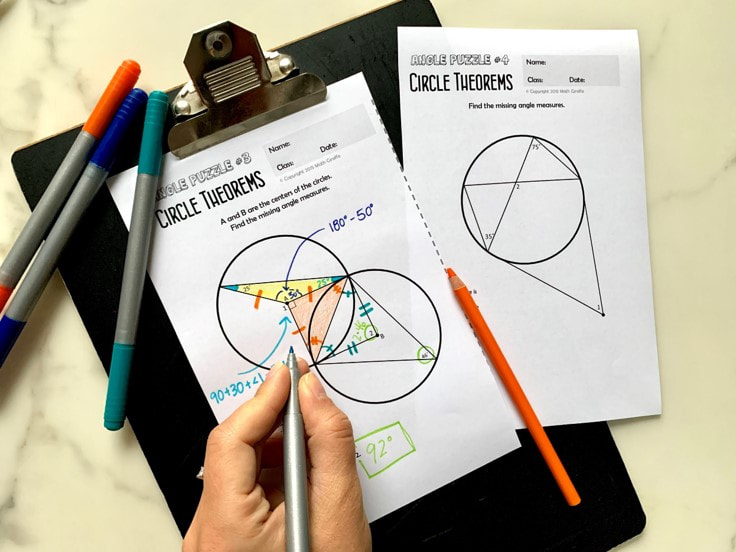
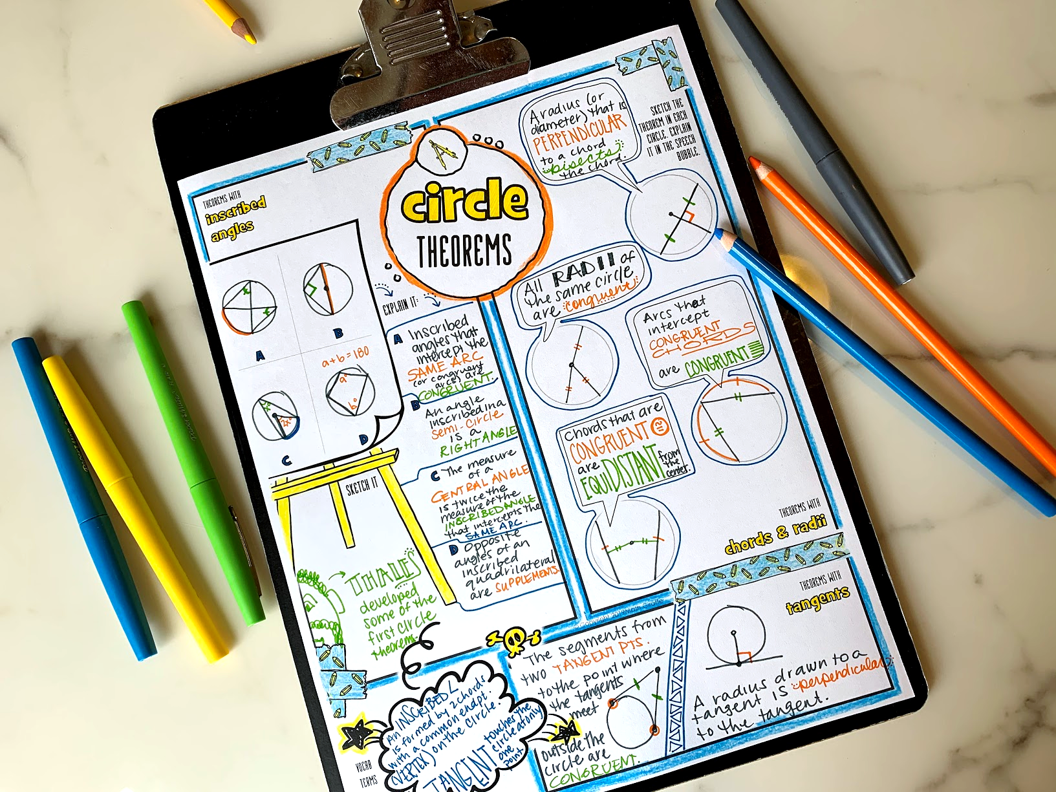
Once students have started having those "aha" moments as they discover the first theorems and are able to start writing rules for what they've observed, you'll eventually want to bring them together as a whole class for some direct instruction. Allow the pairs to share what they discovered. Go over the theorems together. Compare how different teams wrote up the rules. Make sure everyone is on the same page and has correctly written up their discoveries. Then, you can go over the remaining theorems. You can give the rest to them as usual. Students should take notes and ensure they've got the idea. You can provide them with a reference guide as well if you'd like. That can be handy for them as they work through proofs and practice problems later on too. I have one included in my circle theorems kit if you'd like to use the materials shown here. Practice Using the Theorems Before Leading into Proofs Once students are familiar with the theorems, let them try some application problems. Your textbook probably has some basic, boring ones that you can begin with. Do a few in class together, and assign a couple for homework. Then, let your students level up their practice the next day with some fun challenge puzzles. This set has a few different circle theorem puzzles at varying difficulty levels. You can let your class try a couple with partners, then let them take on a more challenging one if they are ready for it. Be careful - puzzle #1 is very tricky. Choose which ones to use wisely ;) Let students see if they really get it Now it's time to test their knowlege with some critical thinking questions. I love using "always true, sometimes true, or never true" questions to see if students really understand the concept well. This type of questioning forces them to test different cases and try to find examples and counterexamples. It's great for building logical reasoning skills, and for seeing where there may be gaps in knowledge. Use always, sometimes, never challenges with partners if you can. They get some really good "math talk" going in the classroom, and then you can go over them as a whole group and check work while addressing the ones that kids got stuck on. The way I designed mine allows for a quick check as you walk around the room. If they've got it, the colors form a secret pattern that you can use to identify any errors at a glance. (But it's not a predictable enough pattern for kids to guess. Very sneaky...) Sum up and review before moving on to proofs Some people like to use their doodle notes as an introduction to a new concept, but a lot of teachers also like them as review. I like blending some of each. You can choose what is best depending on the lesson. And in this case, since the introduction to the lesson was an inquiry activity, the doodle notes make a great sum-up activity to review all the properties / theorems. The circle theorems doodle notes make a great reference guide for students. The creativite aspect helps activate all those magical neural pathways, but also, since they can visualize the layout later on in their minds, they can recall the theorems more easily during a test. This is one of the many benefits of doodle notes. Interacting with the visual notes automatically will activate the brain pathways that lead to stronger retention and also take advantage of the powerful brain hemisphere crossover. Proof Time! Finally the best part - write some proofs with the theorems. The doodle notes you just finished are perfect for pulling back out to have on hand to peek at during proof writing. This is why I like having that step come right before proofs for this unit. They now will have their theorems organized into three categories on that page:
Start with a couple of basic proofs using the theorems with chords and radii. These are a nice beginning point. Then, lead into a couple proofs with inscribed angles next. Then, you can have them try a few on their own before moving on to the theorems with tangents. My big proofs pack has a lot of proofs you can use for this if you need some, or you can just use whatever you've got in your textbook. It's great to have a wide range of proofs that all follow a nice consistent format. Set your students up for success by having the practice proofs organized the same way as the ones on quizzes like those ones are. When you get to the point that you are ready to go more in-depth with the theorems involving tangents, you can use my free diagrams here. This is a nice way to spice it up. You can use the tangent diagrams in so many ways. I like printing them on label paper so they peel off in perfect squares and kids can stick them right into their notebooks. The free sticker templates make that easy. Click on the button below to download them. You'll just print the pages on square label sheets. (Directions and specifics are included in that free download file.) That way, everyone instantly has all the diagrams right in their notes without having to draw them by hand. It saves a lot of time, and they can still mark them up and use color coding. Encourage your students to use color coding to match up lines of proof with colors in the diagram. Their markings will not only help them to go through the logic and steps and keep everything straight, but they'll also help you with grading. As you review the lines of their proof, it's much easier to see where a student went wrong if you can follow their thought process by following their color coding. If you don't have label paper, don't worry. You can still use these tangent diagrams and have options. You can either... 1. Print these free tangent diagrams on full-page sticker paper, and students just will have to cut across to divide up the squares before peeling the stickers. ...or... 2. Print the free diagrams on regular paper. Kids will just have to use a glue stick. It still is a really efficient way for them to get the diagrams right into their notes, just not quite as quick and easy as the label method. You can also use these diagrams just for yourself to easily create worksheets, practice problems, or even quizzes. Just stick a few on the page, write your "given" information alongside it, and photocopy! It makes it super simple to build a quick handout. Have fun teaching circle theorems! For an easy to use pack of all the materials shown here, you can grab the Circle Theorems Bundle here. Hopefully these creative methods and activities will not only help you spice it up and get some variety, but also will build deeper understanding and stronger retention for your Geometry students. More Help for Teaching High School Geometry:
13 Comments
|
Archives
December 2023
Click to set custom HTML
|











 RSS Feed
RSS Feed