|
Help Students Understand Reasoning & Proof by Explicitly Teaching the Distinction in a Way that Textbooks Don't
This concept (accompanied by free downloads below for both middle and high schoolers) gives a boost to students in grades 6-10. This will help set them up for higher level Algebra as well as Geometry and proofs. These skills strengthen reasoning and really have helped my students understand math on a deeper level.
When getting ready to introduce geometry proofs, I have learned that it’s essential to teach transitive property vs. substitution before jumping into proofs with geometry diagrams. This structure is missing from the curriculum I have seen. So, I’ve built my own resources to slowly build these skills that so many students are missing. It has made such a difference for my own classes. Be sure to take time to include these resources (free below) to give your own kids this leg up in Algebraic reasoning! I've put together materials and videos showing the perfect way for you to clearly explain the difference between the transitive property and substitution. This is a tricky distinction for students; so it’s important to be clear right off the bat! Keep reading for the ideal explanation of the difference between transitive and substitution property, and how to effectively prepare your students for Geometry (and higher level Algebra) proofs!
Transitive Property vs. Substitution
This is tricky for our students, so read carefully to make sure you are able to give an effective and clear explanation. I have found it helps to teach this with individual cards for each variable, (See my video, below). For high schoolers, explicitly teach this difference. For middle school, scroll down to the picture puzzles for skill building instead. Substitution: So, let’s say we have 2 given equations: a + b = c and a = g Since a is equal to g, we can replace a with g and make a new equation→ g + b = c When two things are equal, we can replace one with the other, and we know that the equation will still be true. This is the Substitution Property. Substitution is the replacement of one piece. Transitive Property: On the other hand, the Transitive Property is when two numbers, variables, or quantities are equal to the same thing (not necessarily each other right away as the given). Let’s say we have two different equations: x + y = g and x + y = z The key for Transitive Property is that one entire side of the equation has to match. So, it’s not just replacing one piece. In these given equations, because z and g equal the same expression, they must equal each other. z = g z and g must be equal, because they are equal to the same QUANTITY. This is the Transitive Property. It doesn’t work unless the entire side of the equation matches. For example, if the equations were: x + y + m = g and x + y + p = z g would not equal z because the equations do not match. I’ve created a video to show you step-by-step. Consider showing this video to your students as well!
Watch the Video:
Introducing Geometry Proofs Once your students understand transitive property vs. substitution, I like to get them practicing using JUST these properties with a new, transitional style of algebraic proofs, before we jump into geometry proofs. FYI: textbooks don’t seem to teach this; this is just a trick I’ve learned to improve understanding of working with proofs! Most curriculum jumps right from the type of algebra proof that is just solving an equation (justifying each step to get to the solution x = a number) into the first geometry-based proofs. If you find a book that includes this style of proof as a bridge between the standard algebra proof and geometry proofs, let me know! So far, I've had to develop my own in-between practice. These proofs teach students how to COMBINE two previous lines in the proof using the transitive property and/or substitution as the justification. Taking a couple of days to develop JUST this thought process helped my students so much. After practicing these proofs, they had no problem easing into the next level of proofs with Angle Addition Postulate and Segment Addition Postulate. (Click here for a fun worksheet for practicing with these postulates.) This made them ready for what used to be such a huge leap. We avoided all the struggle that usually comes with introducing proofs. They did not feel nearly as lost.
(For these additional free Geometry proof resources, enter your email to subscribe at the bottom of this post. They'll be sent right to your inbox.)
FREE MATERIALS to build these skills
Here are two resources to help you build this skill: 1. My special breed of proofs Include these algebra proofs as a bridge between algebraic and geometry proofs with justifying reasoning just for combining lines using transitive property and substitution. Click here for FREE samples of algebra proofs!
my special breed of transitional proofs
The key is that these are DIFFERENT from the typical “solving” style algebra proof. Look closely!
2. SKILL BUILDING Picture equation puzzles This free set of fun challenge cards can be used in middle school OR high school to help your students build up the knowledge they need for geometry proofs (and algebra reasoning)! This free download comes with 4 basic cards, 4 medium cards, and 4 difficult cards for those students who want a challenge!
free skill-building puzzle sets
The set is differentiated to meet the needs of each of your students at any level.
For more tips on teaching these skills before having students prove their logic, go to Introducing Geometry Proofs! This makes a huge impact on student comprehension, so be sure to download the sample proofs if you just did a quick skim or don’t quite know what I am talking about ? Remember to enter your email below and subscribe to Math Giraffe for more materials, updates, and ideas!
To Read Next:
19 Comments
Ellen Allen
3/30/2018 09:01:09 am
I would like to see your video.
Reply
Lois Coles
8/29/2019 04:12:42 pm
please send the Geometry handouts.
Reply
8/30/2019 12:22:43 pm
Hi Lois.
Reply
Olga Shafran
9/12/2019 10:36:18 am
Thank you so much for this! Very helpful!!
Reply
Pearl Chow
9/14/2019 06:53:32 pm
"It doesn’t work unless the entire side of the equation matches. For example, if the equations were:
Reply
9/15/2019 12:21:17 pm
Hi Pearl,
Reply
Marie
10/1/2019 01:03:11 pm
This is great! It is a great explanation of how to tell the difference between the two. I will be showing my students so they will understand the difference.
Reply
Summer
7/20/2020 11:38:02 am
This video helps a lot to see the differences
Reply
Tisha Saffa
11/11/2021 11:32:35 pm
Thank you for this great video and explanation. I teach eighth grade geometry and my students struggle as do I with the difference between the transitive property of equality and the substitution property. But I am still unsure what to do in the cases like your very last one…
Reply
11/14/2021 10:59:02 am
Hi Tisha,
Reply
Megan
8/29/2023 08:01:19 pm
I'd like to piggyback on Tisha's question, but I'm going to mix it up. I agree that they can use transitive OR substitution in the following example (thanks to your video - thank you - I show it to my class every year, now). 9/5/2023 11:24:00 am
Hi Megan, 1/22/2022 05:15:58 am
This is a wonderful explanation of the differences between them. It is something I am going to show my students in order for them to understand the difference.
Reply
Most geometry books have algebraic proofs, but not those for which you need to combine the previous lines with an alternate or transitional feature. They usually justify you taking steps to solve a one or two-step equation. After that, I highly recommend adding them, which teach these skills how to connect the previous lines as well as new geometry skills later.
Reply
3/1/2022 02:44:33 am
There are so many blog i read right know but any one of them satisfy me but this one is so informative blog.
Reply
Fran
8/8/2023 04:36:13 pm
I really loved reading your blog. Be sure to travel always insured whit <a href="https://www.365sabadosviajando.com/consejos-de-viaje/chapka-seguros/">chapka seguro</a>
Reply
11/22/2023 06:42:59 am
With the rapidly growing influence of Istanbul Airport, the plots in Arnavutk offer a great potential for investors. Arnavutkoy Emlak can help you evaluate these opportunities with land options suitable for every budget and expert consulting services. https://turkishclassified.com/category/turkey-property-for-sale/apartment
Reply
Leave a Reply. |
Archives
December 2023
Click to set custom HTML
|



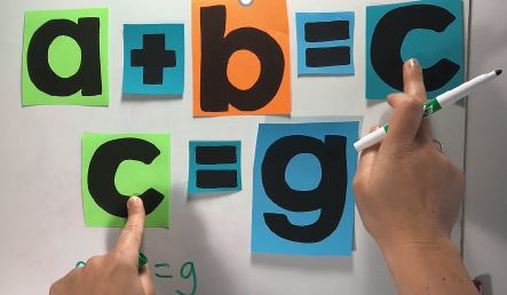






 RSS Feed
RSS Feed