Discovery: Impossible Triangles

This is such a fun way to introduce Triangle Sum Theorem.  This lesson is meant to be inserted right after reviewing the types of angles and triangle classifications (acute, obtuse, right, isosceles, equilateral, scalene).

Setup (Behind the Scenes)

Start by downloading a Geometry Software program (You can do this for free!)

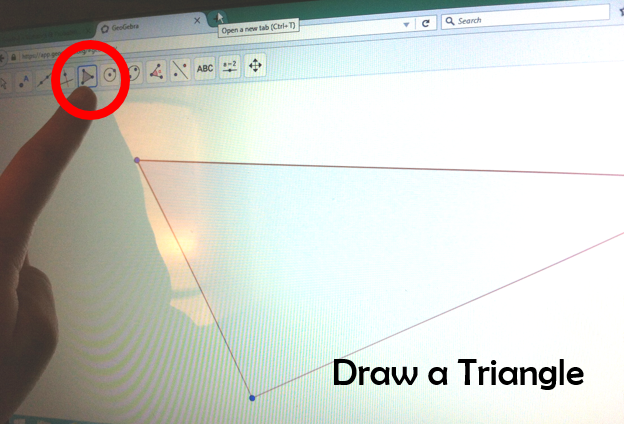
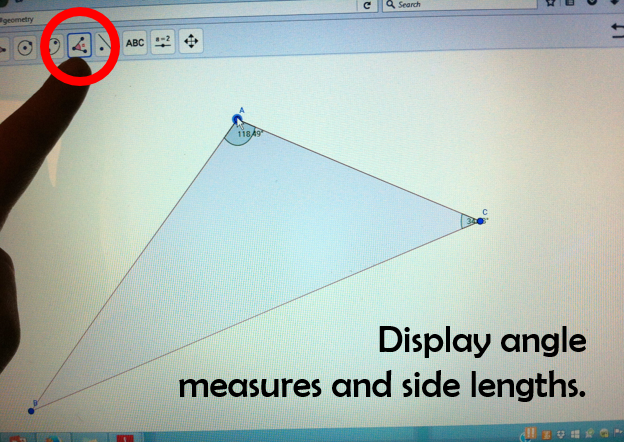
Draw a quick triangle using the software and display each side length and angle measure.  These will adjust as a vertex is dragged.   Here are shots to show you how it looks in GeoGebra.  The triangle/shape button is first, then use the angle measure button to mark off the three points that name each angle.  (Do 3 times to get all 3 angles marked.)

That's it for setup!  Once you get the hang of it, setting up an easy hands-on virtual discovery with GeoGebra only takes a minute.

The Lesson - Phase 1:

I set the stage as if we are just going over the triangle classifications we just reviewed.  I let one student at a time come up to manipulate the triangle. This works great on a smartboard or with a computer and projector.

 Ask the first student to drag a vertex to make the triangle a right triangle. He or she will drag a vertex and move things around until they can get one angle measure to be 90 degrees.  Success!  Then have another student come up.  The kids love this, and are so excited to play with the geometry software for the first time.

Calling up one student at a time, have them create a few basic types of triangles (something like an acute isosceles triangle, and then an obtuse isosceles triangle, and then even a right isosceles triangle).

Once you have been through a few of these successfully, give the next student a challenge to create a "right equilateral" triangle.  Do not hint that it cannot be done. Some students may figure out that it is impossible after just a minute and giggle as the student tries dragging a vertex different ways. 

Eventually, you can allow them to explain why they think the student at the board should give up. Continue on with some possible and some impossible triangles.

Request the following triangles:

• right isosceles
• obtuse scalene
• obtuse equilateral
• right obtuse
• etc....

This leads to really great discussions. As an extension, you can have students list as many impossible triangles as they can.  Let your class explore and investigate triangles using the software.  Allow students to explain WHY certain triangles are impossible.

The Lesson - Phase 2:

Ask students to write a theorem stating what they discovered.

Try other hands-on activities exploring triangle sum theorem.  One option is to have students draw a large triangle, rip off all three vertices, and line them up in a row.

You can also have students use a protractor to measure the angles.  Allow them to work in pairs to write an official theorem.

Join together as a whole class to discuss and make sure that all pairs understand.

Click here for the lesson pack of worksheets that I use to accompany this lesson.  There are materials for writing up the theorem, directions for cutting up a triangle, warm-ups, practice, and more.

Next Lesson:

Once your students have a good grasp of Triangle Sum Theorem, and get in some practice, move on to Triangle Inequality Theorem.  I start this one out by asking them to move the desks into a certain arrangement (that turns out to be impossible once they try to line them up!)  Read about structuring that lesson here.

To read more and get freebies and updates, subscribe to the Math Giraffe email list.  Just enter your email in the sidebar.

To Read Next: