How to Teach Geometry Proofs

Writing Two-Column Proofs: A Better Way to Sequence Your Proof Unit in High School Geometry

Leading into proof writing is my favorite part of teaching a Geometry course.  I really love developing the logic and process for the students.  However, I have noticed that there are a few key parts of the process that seem to be missing from the Geometry textbooks. 

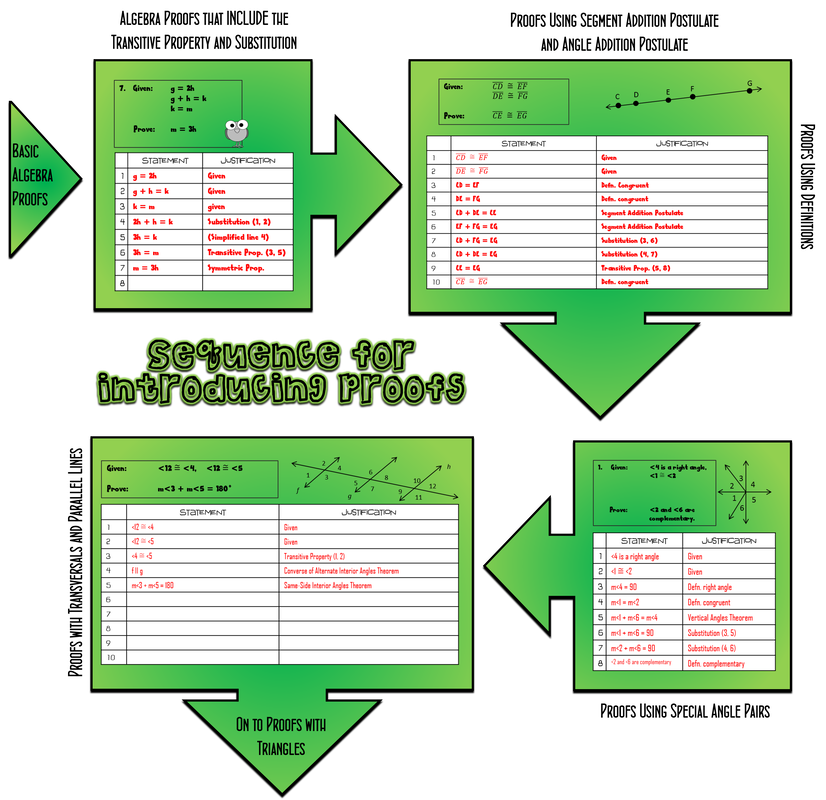
I started developing a different approach, and it has made a world of difference!  

The Old Sequence for Introducing Geometry Proofs:
Usually, the textbook teaches the beginning definitions and postulates, but before starting geometry proofs, they do some basic algebra proofs. Most curriculum starts with algebra proofs so that students can just practice justifying each step.  They have students prove the solution to the equation (like show that x = 3). 

That's fine. It's good to have kids get the idea of "proving" something by first explaining their steps when they solve a basic algebra equation that they already know how to do. 

But then, the books move on to the first geometry proofs. And I noticed that the real hangup for students comes up when suddenly they have to combine two previous lines in a proof (using substitution or the transitive property).  

They get completely stuck, because that is totally different from what they just had to do in the algebraic "solving an equation" type of proof. It does not seem like the same thing at all, and they get very overwhelmed really quickly.

The standard algebraic proofs they had used from the book to lead into the concept of a two column proof just were not sufficient to prevent the overwhelm once the more difficult proofs showed up. Solving an equation by isolating the variable is not at all the same as the process they will be using to do a Geometry proof.

A New In-Between Step:
So, I added a new and different stage with a completely different type of algebra proof to fill in the gap that my students were really struggling with.  First, just like before, we worked with the typical algebra proofs that are in the book (where students just justify their steps when working with an equation), but then after that, I added a new type of proof I made up myself.

I led them into a set of algebraic proofs that require the transitive property and substitution.  This way, they can get the hang of the part that really trips them up while it is the ONLY new step! We did these for a while until the kids were comfortable with using these properties to combine equations from two previous lines.

My "in-between" proofs for transitioning include multiple given equations (like "Given that g = 2h, g + h = k, and k = m, Prove that m = 3h.") Instead of just solving an equation, they have a different goal that they have to prove. Their result, and the justifications that they have to use are a little more complex.

This way, the students can get accustomed to using those tricky combinations of previous lines BEFORE any geometry diagrams are introduced.  They are eased into the first Geometry proofs more smoothly.  This extra step helped so much.  After seeing the difference after I added these, I'll never start Segment and Angle Addition Postulates again until after we've practiced substitution and the transitive property with these special new algebra proofs.

Here are some examples of what I am talking about. The books do not have these, so I had to write them up myself.
(I am sharing some that you can download and print below too, so you can use them for your own students. There are also even more in my full proof unit.)

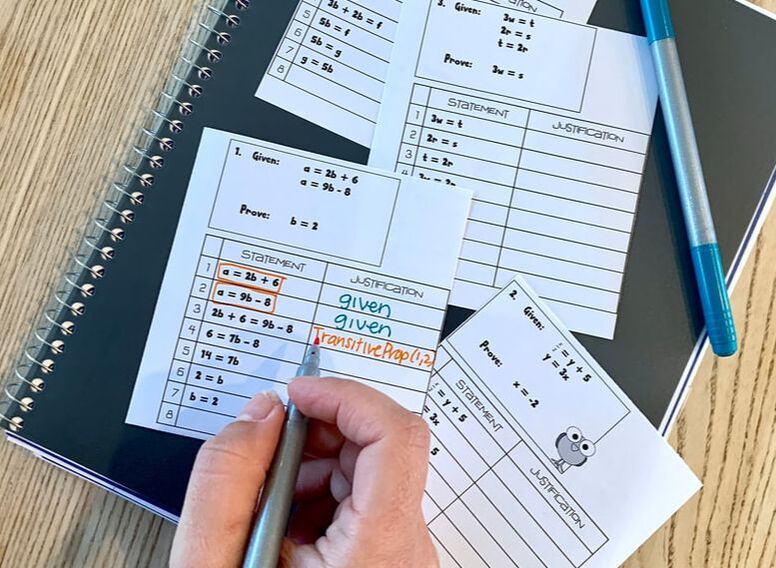
Do you see how instead of just showing the steps of solving an equation, they have to figure out how to combine line 1 and line 2 to make a brand new line with the proof statement they create in line 3? 

You can start with ones like this (above), where the statements are already provided and they just have to fill in the second column, and then as usual, after that you will want to lead into some where both columns are blank and they have to come up with the entire thing themselves.

Here is a close-up look at another example of this new type of proof, that works as a bridge between the standard algebra proofs and the first geometry proofs.

The way I designed the original given info and the equation that they have to get to as their final result requires students to use substitution and the transitive property to combine their previous statements in different ways.

Practicing proofs like this and getting the hang of it made the students so much more comfortable when we did get to the geometry proofs. It saved them from all the usual stress of feeling lost at the beginning of proof writing!

Here is another example:

Sequencing the Proof Unit with this New Transitional Proof:
After finishing my logic unit (conditional statements, deductive reasoning, etc.), I start (as most courses do) with the properties of equality and congruence.  I also make sure that everyone is confident with the definitions that we will be using (see the reference list in the download below).  I introduce a few basic postulates that will be used as justifications.  I spend time practicing with some fun worksheets for properties of equality and congruence and the basic postulates.

Then, we start two-column proof writing. The usual Algebra proofs are fine as a beginning point, and then with my new type of algebra proofs, I have students justify basic Algebraic steps using Substitution and the Transitive Property to get the hang of it before ever introducing a diagram-based proof. 

The flowchart (below) that I use to sequence and organize my proof unit is part of the free PDF you can get below. The PDF also includes templates for writing proofs and a list of properties, postulates, etc. that I use as a starting point for the justifications students may use.

The extra level of algebra proofs that incorporate substitutions and the transitive property are the key to this approach.

This addition made such a difference!  By the time the Geometry proofs with diagrams were introduced, the class already knew how to set up a two-column proof, develop new equations from the given statements, and combine two previous equations into a new one. 

Another Piece Not Emphasized in Textbooks:​
Here's the other piece the textbooks did not focus on very well - (This drives me nuts).  Please make sure to emphasize this -- There is a difference between EQUAL and CONGRUENT.  This is a mistake I come across all the time when grading proofs. It may be the #1 most common mistake that students make, and they make it in all different ways in their proof writing.

​I make sure to spend a lot of time emphasizing this before I let my students start writing their own proofs.  I make a big fuss over it.  I require that converting between the statements is an entire step in the proof, and subtract points if I see something like "<2 = <4" or "<1 + <2 = <3".

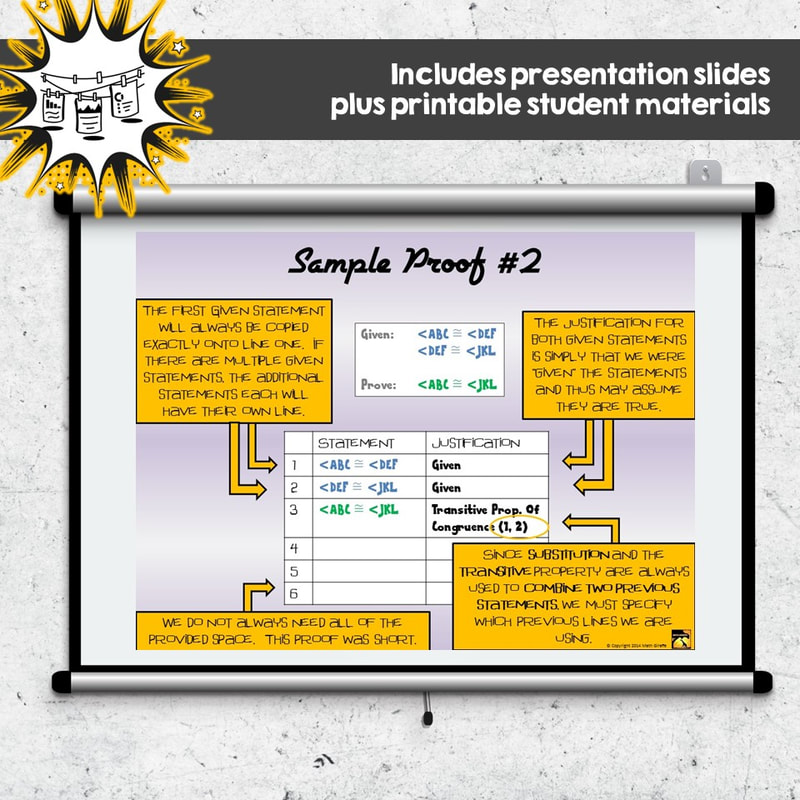
(The slides shown are from my full proof unit.)

When It's Finally Time for Geometry Diagrams:
In the sequence above, you'll see that I like to do segment and angle addition postulate as the first geometry-based two column proofs. Real-world examples help students to understand these concepts before they try writing proofs using the postulates. 

Guided Notes:

When you introduce the proof writing process itself, it's nice to have guided notes that students can keep as a reference. Interactive doodle notes are perfect for this because they blend words and imagery to help students retain the information and visualize it as a clear process in their minds.

The doodle notes I created for teaching Geometry Proof Writing are available here if you'd like to use these to accompany your proof lecture.

This way, they can solidify the concept, build mental connections by blending visual and text info, and then have a reference that they can pull out when they are studying or when they are trying a practice proof and get stuck.

After practicing with those transitional proofs I added, my students finally did not have a problem easing into the next level of proofs with Angle Addition Postulate and Segment Addition Postulate.  This made them ready for what used to be such a huge leap with other classes.  We avoided all the struggle that usually comes with introducing proofs.  They did not feel nearly as lost.

​When we finally got into the good stuff, after watching me demonstrate a few proofs, a lot of kids would say things like...

“Ok I kinda get what you are doing, and each step makes sense, but you are just making it look easy.  It seems like you're just making it up."

or

"I understand some of where it is coming from, but there is just NO WAY I could come up with these steps myself and get from the beginning to the end on my own.”

Posters as a Guide for those "I'm Stuck" Moments:
To help them organize the procedure and get "un-stuck" when they were unsure how to progress to the next step, I developed a series of steps for them.  Some kids really depended on this, and some thought that it didn’t help much.  For students who do need that structure, though, this chart can be their friend on their desk at all times for the entire month as we progress through the unit.

​Another group of students seemed to need a reference list of what kinds of things can be used as justifications.  Proofs are so different from anything that has been done before in their math classes.  Each student seems to get stuck on a different part of the process.  I found that having a reference sheet helped them a lot.

They can add to this sheet as they learn more postulates and theorems later on until they no longer need a list.

DOWNLOAD these POSTERS for FREE:   Printable versions of these two pages are included in an email that I send out to subscribers.  If you would like to have the 8.5x11 posters for your students, subscribe to the Math Giraffe email list, and they will be sent straight to your inbox as part of the toolkit for teaching math!

Enter your email address here to get the pieces shown above sent to your inbox:

(An additional free download is available below, so scroll down for the printable download of the special algebra proof samples too!)

Next, we move on to proofs with special angle pairs (supplementary angles, vertical angles, etc.) From there, things tend to smooth out. It gets easier to introduce each new type of proof, because all that is changing is the theorems that we use as we lead into proofs with triangles. 

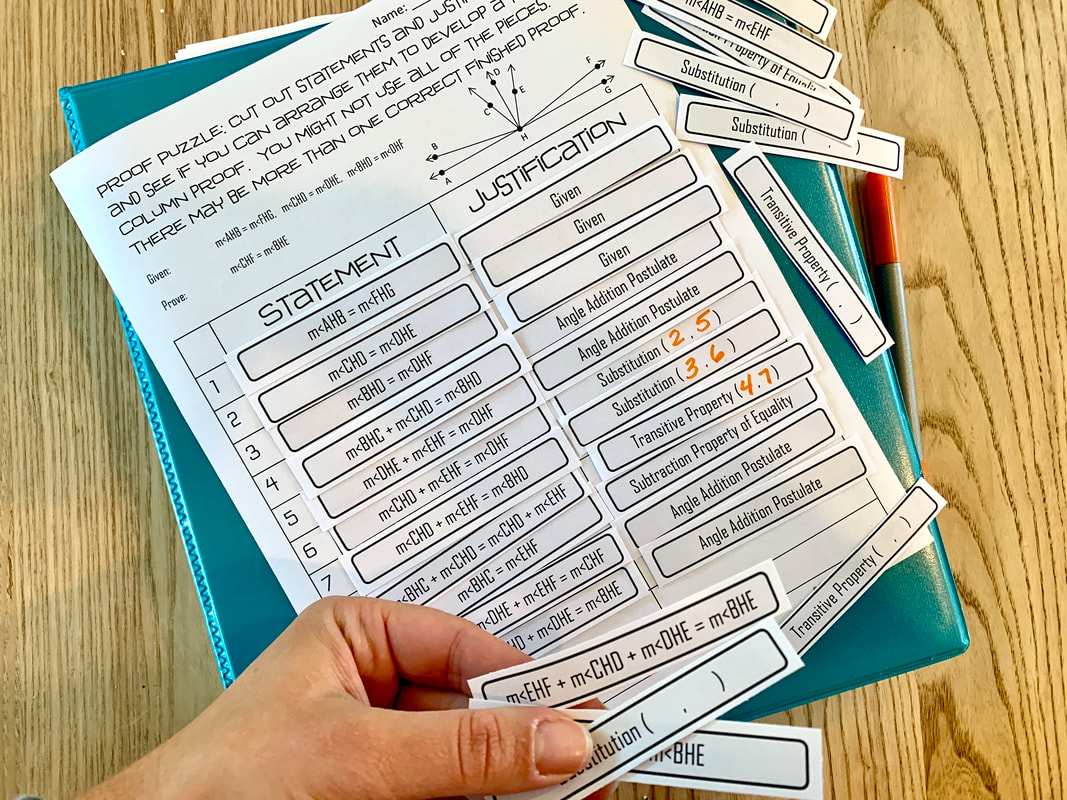
The format of stepping through a puzzle and getting to the end of the proof stays the same. It's best to keep the structure well-organized and the same throughout. I keep a template handy with my 2 columns in the same format, so I can just fill in the blank space at the top and copy it for any new type of proof. The students can feel the familiarity of the columns and structure all throughout the course.

Try it - Free Download
You can use this sample set to try these algebra proofs in your own classroom.  You'll love the way this additional lesson leads your students into proof writing more smoothly.  This PDF includes a few examples that are half-sheet size.  They work really well as warm-ups.

If you like this format and would like my full Proof Unit, it's available here:
FULL Geometry Proof Unit: Presentation & Printables

Click the images for more information.