KEY SKILL: Teaching Students to Test Cases And Use Examples & Counterexamples in Math Class

In a high school Geometry course, we teach examples and counterexamples along with conditional statements and logical reasoning.  But this piece is a missing key before kids get to that stage.  It's not really an automatic part of Pre-Algebra or Algebra 1.

After noticing kids with a lot of trouble thinking critically to determine whether statements are true or false, I've realized that we need to expand the explicit teaching of examples and counterexamples beyond Geometry class.

In almost every topic of study throughout their math courses, kids can benefit from practice and instruction on this skill.

They need to be learning how to test different cases, organize information, and draw conclusions about the math properties that are at play.

The easiest and most concrete way I've found to do this is through "always, sometimes, never" questioning.

Kids cannot think through these types of questions without mentally testing cases.  And if you go a step beyond to have them support their answers, they will be forced to justify by using both examples and counterexamples.  

BONUS: This type of question almost ALWAYS inspires some solid "math talk," so make sure to let your classes work in pairs or showcase their reasoning at the board to get that conversation going.

Here are some examples to try to incorporate:

Testing Cases in Algebra:

Often, students may think they know the answer and then in testing, they'll come across a different situation that violates the "rules" they were imagining originally.

Make sure to have them try every case they can think of that fits the "premise" criteria and then see if they can reach a conclusion about whether each statement is always true, sometimes true, or never true.

Samples with Quadratics:  Always true, sometimes true, or never true??

• The graph of a quadratic function with a positive linear term crosses the x-axis.
• A quadratic equation contains no negative terms and has two real solutions.
• A quadratic equation with a negative leading coefficient is represented by a parabola opening upward.

(more quadratics questions)

Pre-Algebra Examples:

Have kids try these samples, and be sure that they support their claims by providing both examples and counterexamples.

See if they can develop some systems to organize their work and be sure that they have tested every possible case.

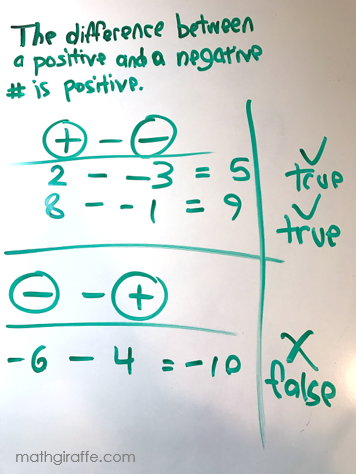
Samples with Integers:  Always, sometimes, or never true??

• The quotient of two nonzero integers is negative.
• The sum of three negative integers is negative.
• The difference between a positive and a negative number is positive.

(more integer questions)

Students will need to test in different orders and justify their answers by showing each case and whether it turned out to be a true or false statement.

Geometry Challenges:

These ones work well at the board, because students can watch one another draw the figures and see which cases work out.  

If you have access to geometry software like GeoGebra, you can use that as well.  Have students draw each triangle and see if they can drag a vertex to meet the criteria.

Samples with Triangles:  Always, sometimes, or never true??

• ​A triangle has two right angles.
• A right triangle is not scalene.
• A scalene triangle has two acute angles.

(more triangle questions)

Best Ways to Try It:

All the sets I develop with this type of questioning include 36 statements to classify.

My favorite 2 ways for students to work through these types of questions are in partners in a worksheet, or as teams with a sorting activity with a notebook on the side.

PARTNER WORKSHEET:
I lay the statements out in a grid so that when they color each statement that is NEVER true RED, each statement that is ALWAYS true BLUE, and each statement that is SOMETIMES true PURPLE, it creates a pattern that I can check really easily in just 2 seconds.

​This makes it really easy to check it over as I walk around and just point to ones that I can see are incorrect.  They go back to the drawing board on those statements and continue their (sometimes heated) discussions!

(Fractions, Decimals, Percents version)

SORTING ACTIVITY:
I cut the statements (larger print version) into cards and have small teams or pairs of students sort them into categories based on whether they are always, sometimes, or never true.  

Be sure that they have notebooks available, because at any moment they may be required to provide examples to support their answers.  

You can also hand out the cards and have students come up to the front in a whole-class setting to tackle challenging ones.  These are pretty versatile.  It's nice to hear a student model an explanation and show the class how they tested different cases to reach a conclusion.

Get Pre-Made Sets

Each time I develop a set, I pull together my worksheet version and my sorting version so both are included.

Browse the sets that will work well for your classroom and get your kids thinking critically!

Pre-Algebra:

• Fractions, Decimals, and Percents
• Integers

Algebra:

• ​​Linear Equations
• Quadratic Equations
• Polynomials

Geometry:

• Quadrilaterals
• Triangles
• Circle Theorems
• Conditional Statements
• Special Angle Pairs
• Points, Lines, Planes, & Angles

Get Inspired:

To Read Next: