23 Ways to Use Dice in Math Class

How can you bring some hands-on spontaneity into your math classroom?  It’s super easy! Invest in some dice and get some inspiration below.
 
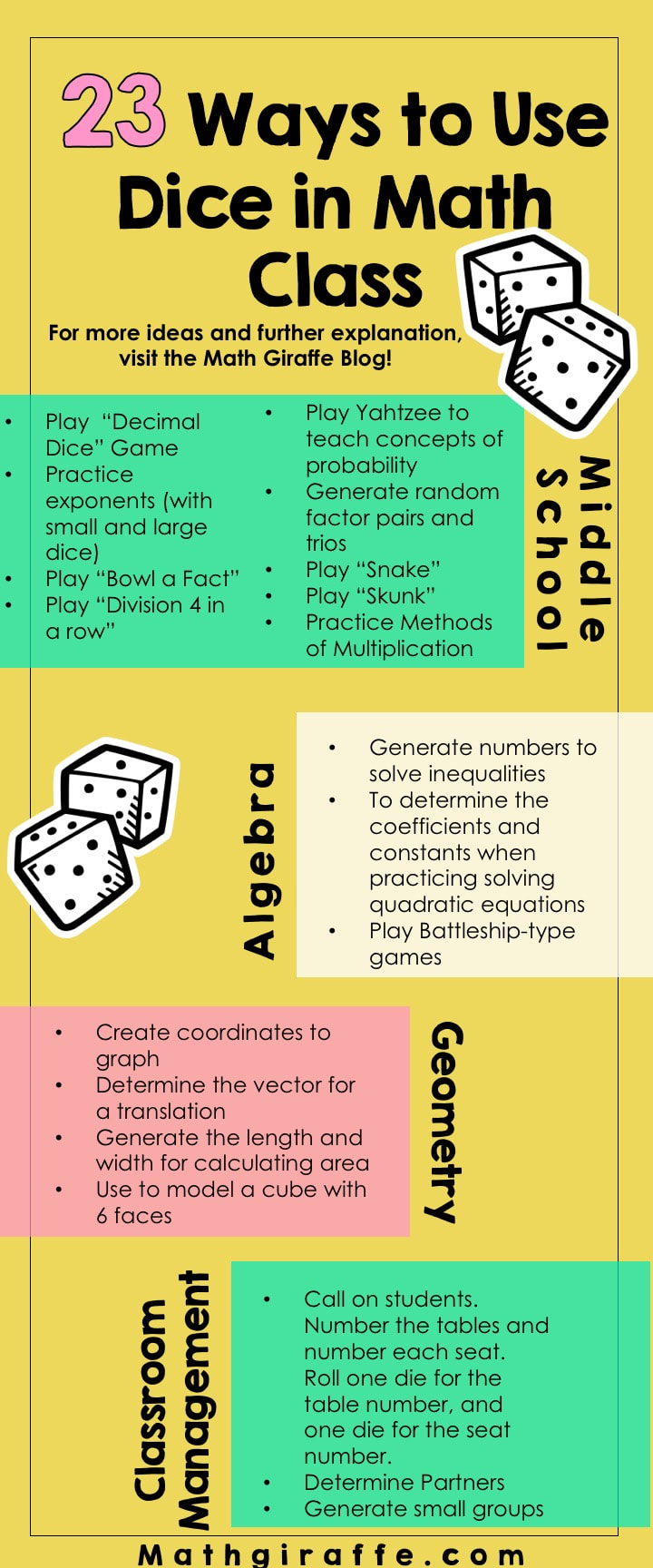
When you make math more hands-on, you not only more successfully engage your students, but you are helping the learning stick in their brains; retention is improved.
 
When you think of math manipulatives, you may think of elementary students using various number blocks to learn place value or addition and subtraction.  Sometimes, we struggle to think of ways to incorporate manipulatives in the upper grades.
 
That’s where dice come into play.  There so many creative ways to get your students using dice in math class.  I like the soft foam dice (shown above) because they are so nice and quiet when rolled!  There are a few options of sizes, which is also nice.  Some of the ideas below require both small and large dice together.  You can also get giant inflatable dice.  By buying just two of those jumbo ones, you'll be able to roll them in front of the whole class for management ideas (below) or for large group lessons on probability, etc. for everyone to see.
 
I posted on Instagram and asked everyone to share their favorite ways to use dice in the classroom, and I’ve included some of my own!
 
Here are 23 ways to get you started.  You can use dice to:
 
 
Middle School Pre-Algebra

• Play a “Decimal Dice Game (@middleschoolmathmoments wrote an awesome blog post about it here.)
• Toss two dice to each student around the class and when they land in their hands, whichever numbers are facing up they have to multiply (@knowledgeovergrades)
• Play a Probability Game (@middleschoolmathmoments)
• Practice with exponents (@maekkan) using small and large dice
• Generate random factor pairs or trios.  (@ez526)
• Practice methods of multiplication (@mia_dor_jet)
• “Bowl a Fact” -a game,(recommended by @melkob124), where students practice combining number combinations to get specific results.  You can find directions at youcubed.
• Play “Division 4 in a Row”- a game to practice division fluency.  You can find directions, here, from multiplication.com.
• Play Yahtzee to teach concepts of probability.
• Play “Snake”- a whole class game to practice multiplication facts, (recommended by @haileygarrou).  Find directions here. 
• Play “Skunk”- a game to teach probability and risk, (recommended by @algebrathecat)

 
 
Algebra

• Generate numbers to solve inequalities (@mia_dor_jet)
• Use them to determine the coefficients and constant when practicing solving quadratic equations using the quadratic formula (@ms.melissa.moreno)
• Play Battleship type games (@maekkan)
• Try @rockymountainclassroom ‘s math trick, and then let students create their own! 

​Geometry

• Create coordinates to graph (@math.with.mrs.n)
• Create the vector for a translation (@math.with.mrs.n)
• Generate length and width for calculating area (@math.with.mrs.n)
•  Use a die as a model of a cube with 6 faces (@doitjewett87)  This one might be simple, but it is so important for students to really hold and visualize it to help them with nets and surface area.
• Determine a scale factor (@garberteachesmath)

 
 
 
Classroom Management

• Call on students. Number the tables and number each seat.  Roll one die to pick the table and another to pick the student (@eweir26)
• Determine partners (@maekkan)
• Generate small groups

 
 
 
Do you have any cool ways to use dice in your classroom?  Add more to this collaborative list in a comment below!

For more ideas, updates, and free printable math materials, enter your email address in the box:

To Read Next: