|
This post has been updated. Read it here, and get all the goodies to print and use in your own Geometry classroom: How To Teach Geometry Proofs: A Better Way to Sequence Your Two-Column Proof Unit
21 Comments
How often do those 3 or 4 kids just seem to be zoned out? These tips will help to draw them back in and keep them on their toes.
The ideas will also help you keep the attention of the entire class. Tip #1: Use an attention signal
Tip #2: Re-focus with color switches, fresh starts, and seat rotations
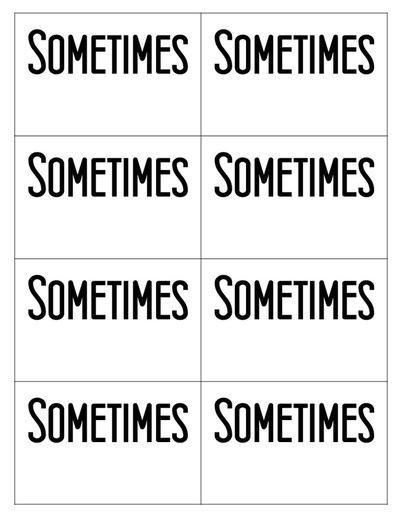
Tip #3: Use student response cards
Download student response cards here. Print on colored paper so you can identify responses at a glance.
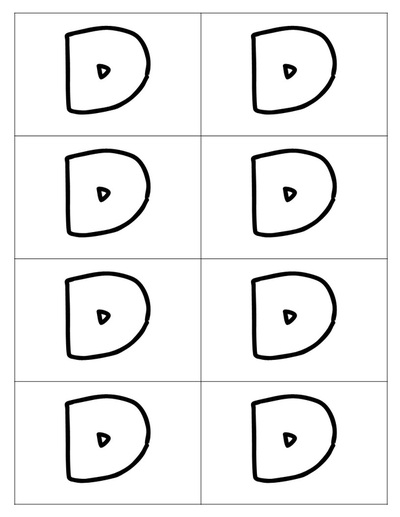
Tip #4: Have students "tag" ideas
Students love to be "woken up" by a call to the board to do what I call a "slap-on" to show that they have been paying attention. You can have them identify key vocabulary, the most important points, common mistakes, formulas, and more!
Add some action to your daily notes!
Grab the download: printable "slap-on" tags for your board. Tip #5: Squeeze in! Accommodate everyone at the board
In a classroom with boards all along two walls, I have had success with bringing the entire class at the board all at once. I notice a big difference in attention and motivation when students work at the board. No one is uncomfortable having their work "on display" if everyone is there together. They are more likely to ask for help as you walk around because their work is visible. The students really enjoy this format and are much more engaged.
Feel free to leave a comment to share your own ideas for increasing student engagement! To Read Next:
|
Archives
December 2023
Click to set custom HTML
|






















 RSS Feed
RSS Feed